这些问题都能从数学找到答案。
在足球运动早期,足球场有多大,取决于人们能找到多大的场地。后来人们意识到:足球场必须足够大,至少要保证不是从任何地方都能射门得分。后来,足球加入了商业因素,就要让球场大小能够容纳足够多的观众,同时保证每一位观众都能够看清比赛。最终,标准足球场被设计成长度大约100米,宽度大约70米的长方形。
那么,比赛人数又该如何确定呢?足球比赛要紧张刺激,就要求对球员形成压力,也就是球员接球之后,必须马上决定如何处理,也就是一个对方球员跑向控球球员的典型时间,必须与控球方接下、控制、移动足球的时间接近。如果球员人数太少,距离太远了,比赛不够紧张。如果球员人数太多,距离太近了,球员来不及思考,足球比赛就会像弹珠游戏一样。
假设足球场的面积为S,每一只队伍有N名球员,平均来讲,每一名球员占有的面积就是S/N。
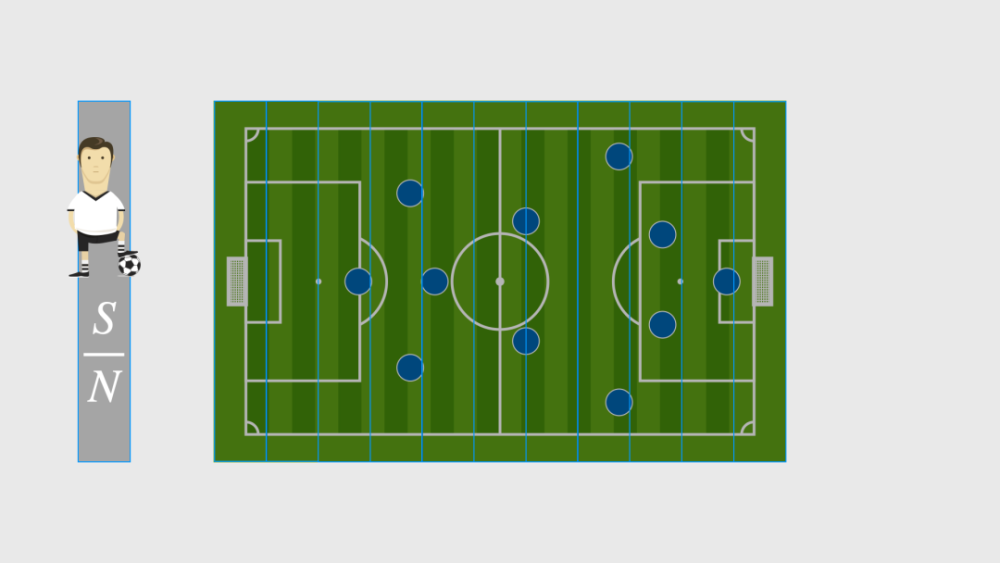
假设这个面积是一个正方形,那么正方形的边长,也就是球员的平均距离d就等于√(S/N)。
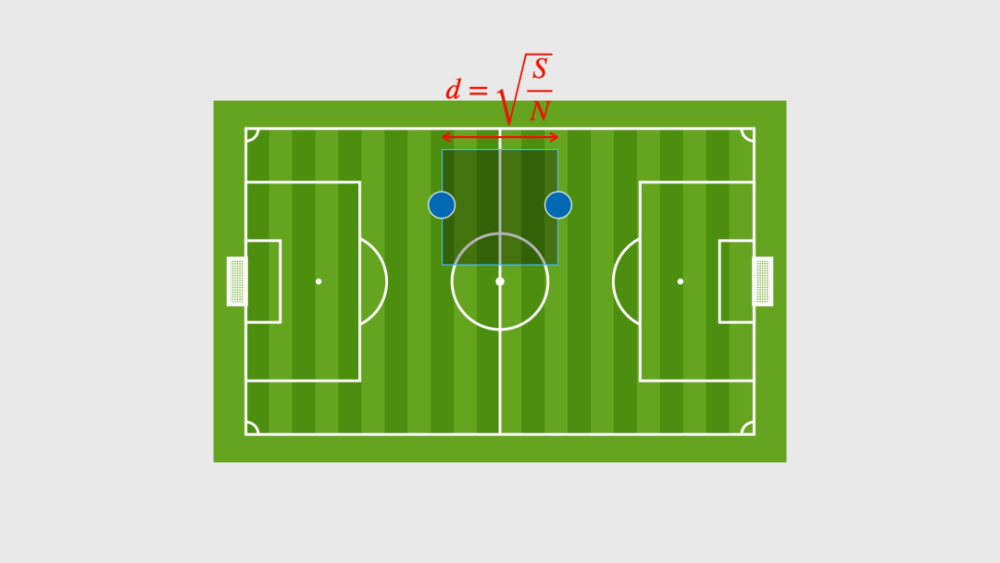
现在,如果有一名对方球员控球,他与防守方球员的平均距离接近d/2,如果球员的速度是v,那么对方球员跑向他,大约需要的时间是d/2v,也就是t约等于1/(2v)*√(S/N)。
如果足球运动员奔跑的平均运动速度是v=5m/s,我们又知道足球场的面积大约S=7000㎡,就能把这个公式简化成t=8.4/√N。
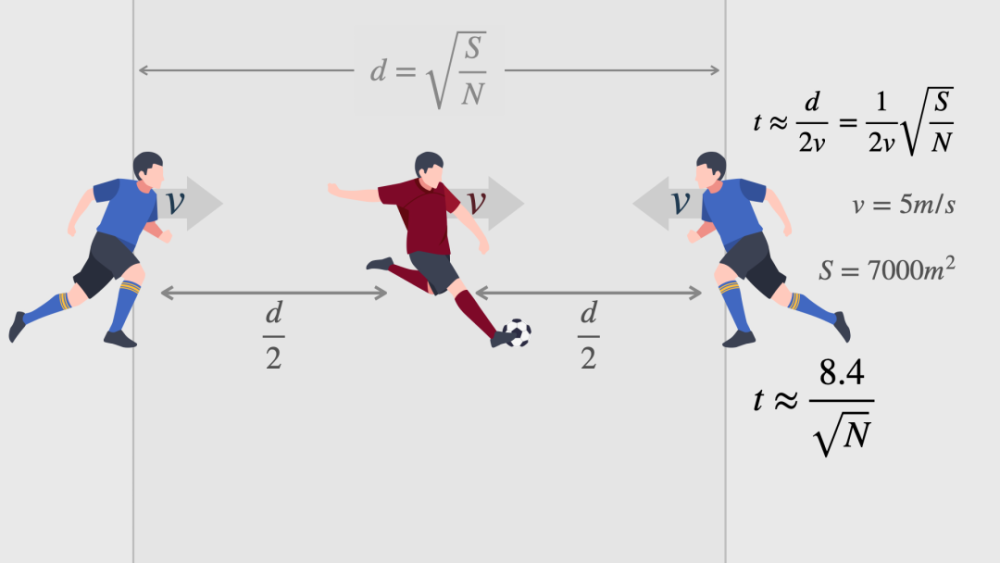
画出图像,你会发现随着每一支队伍运动员人数N的增加,留给球员的控球时间t就越来越小。
在每支队伍11人的时候,留给每名球员的反应时间大约2.5秒,他可以用1秒停好球,1秒钟控球、观察周围环境和思考,下一秒就需要开始盘带或者传球了,这样的比赛既有节奏,又精彩刺激。每队11人,是一个合理的结果。
其实,像这样的设计,在足球比赛中还有很多。比如为什么点球要在球门前11米的地方罚呢?
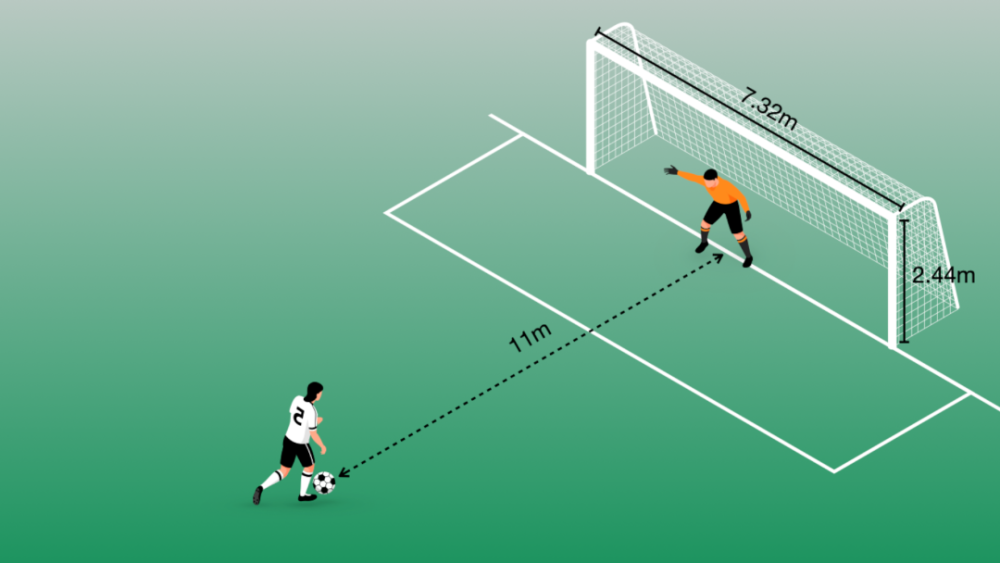
足球运动员踢出的点球速度可达100km/h,在11米的球门前罚点球,就算飞到最远的球门角落,只需要大约0.4s。如果守门员的扑救速度是每秒钟6-7米,考虑到守门员的身高、双臂的长度和球门的尺寸,他大约需要运动2米才能覆盖住球门的角落,需要大约0.3秒的时间。也就是:守门员最多只有0.1秒的反应时间,这对于一般人来讲都是不够的。
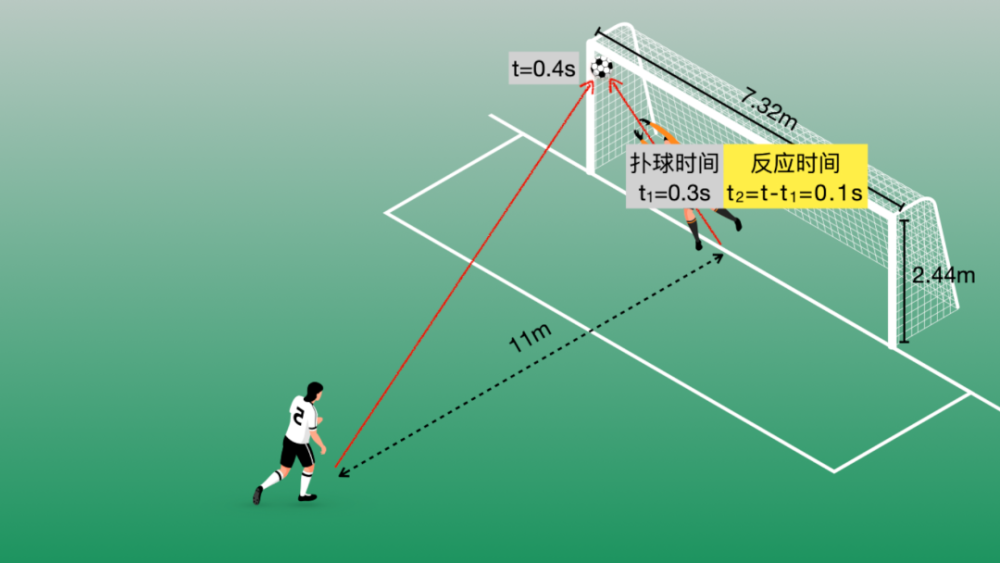
所以,守门员必须在球被踢出之前猜测对方踢球的方向,然后提前移动,只有猜中了球的方向,才有可能把点球扑出。
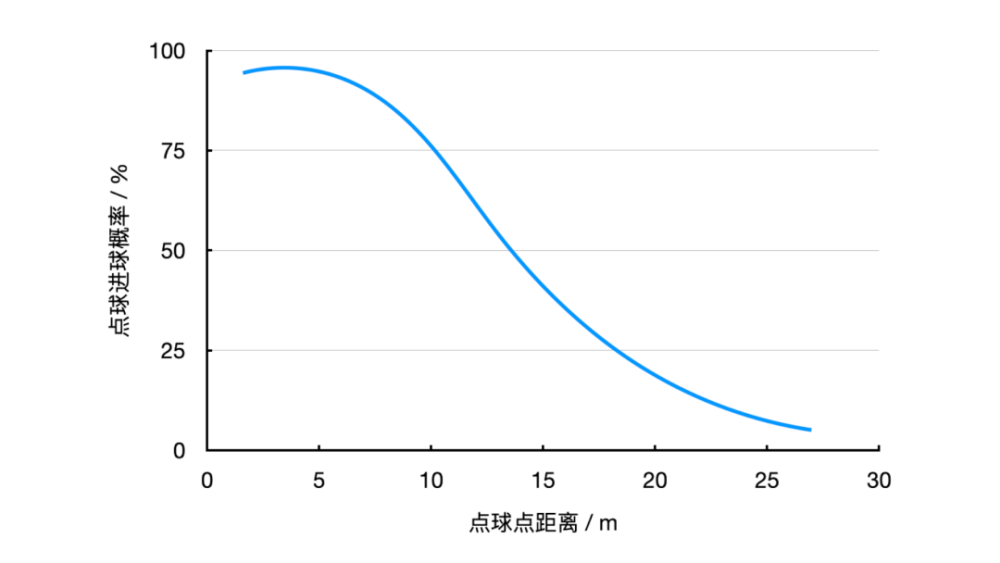
经过实验,人们发现:罚球点距离球门越近,点球命中率越高,距离为3米左右时,命中率几乎为100%,罚点球和罚分一样,就没意思了。罚球点距离越远,点球命中率越低,超过20米时,命中率不到20%,这也就失去了惩罚的意义。所以人们才设计了11米这个罚点球的位置,这时点球命中率大约70%,世界杯的数据也支持了这个结果。
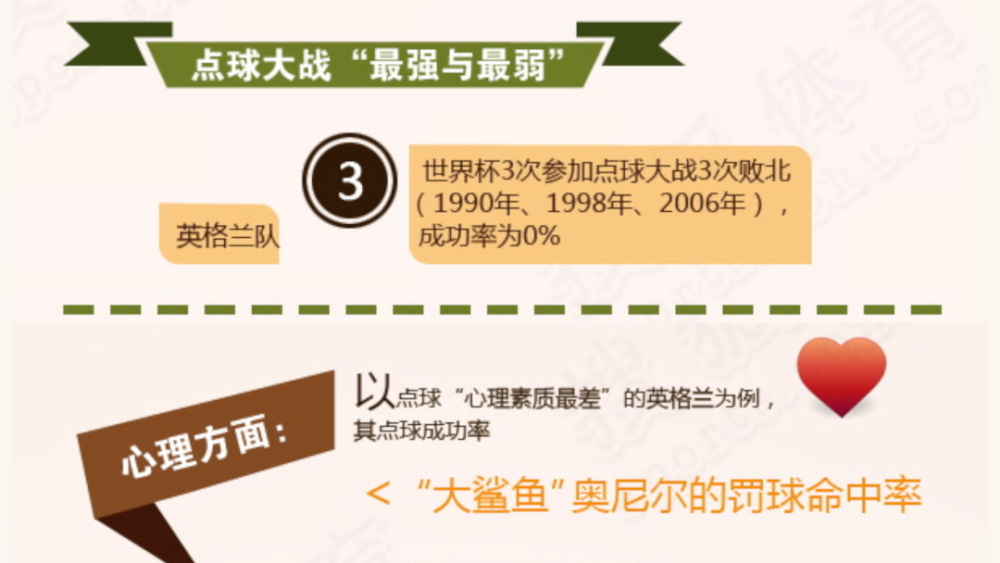
当然,英格兰这种点球大战时心理素质奇差,命中率低于奥尼尔罚篮命中率的球队也是有的。
在1891年,人们设计罚点球规则时,可能并没有经过我们这么多计算,但是人们的确找到了一个最合理的距离,70%的命中率让点球大战也能充满未知。


